"É impossível pentear uma bola coberta de pelos de forma que não existam buracos ou redemoinhos"
Um enunciado mais formal para este fato é o que se segue:
"Todo campo vetorial contínuo tangente sobre a esfera terá um ponto de singularidade."
Este teorema foi enunciado no final do século 19 pelo matemático Henri Poincaré (Imagem acima à esquerda) e uma prova rigorosa surgiu em 1912 com Luitzen Brouwer (Imagem acima à direita).
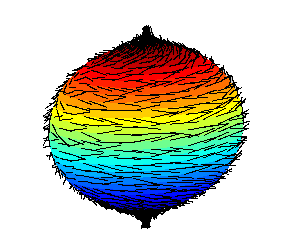
Podemos imaginar um campo vetorial contínuo tangente sobre a esfera como o movimento de um pente que não é retirado da superfície durante o processo de penteação e consequentemente esse campo possuirá um ponto de singularidade,que pode ser relacionado à um "tufo de cabelo" ou um "redemoinho", abaixo se segue uma tentativa frustada de pentear uma bola cabeluda:
 |
| Wikipédia |
Um campo de vetores tangentes sobre uma superfície em $\mathbb{R}^3$ é uma aplicação que associa cada ponto sobre essa superfície à um vetor tangente nesse ponto. No nosso caso, tomando a esfera tridimensional $\mathbb{S}^2$ como essa superfície, definimos um campo vetorial contínuo tangente como a seguinte aplicação contínua:
$$T:\mathbb{S}^2\rightarrow\mathbb{R}^3$$
onde cada ponto $p\in\mathbb{S}^2$ associamos um vetor tangente $T(p)\in\mathbb{R}^3$. Podemos então enunciar o teorema de outra forma:
"Se $T:\mathbb{S}^2\rightarrow\mathbb{R}^3$ for um campo vetorial contínuo tangente sobre a esfera, então $\exists p\in\mathbb{S}^2$ tal que $T(p)=0$."
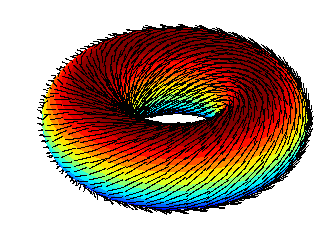
Um fato curioso é que esse mesmo processo é possível em uma rosquinha peluda, ou seja, é possível definir um campo vetorial contínuo tangente pela superfície de um toro, abaixo você pode visualizar um "penteado" em um toro:
 |
| Wikipédia |
1) Se tomarmos a Terra como uma esfera (no ponto de vista topológico a terra e a esfera são a mesma superfície!) e os ventos como campos vetoriais contínuos tangentes, então podemos afirmar que em algum momento algum ponto na superfície terrestre não estará ventando!!! No ponto de vista físico isso quer dizer que sempre existirá um ciclone na superfície da terra, e isso ocorre pelo simples fato de nosso planeta possuir uma forma esférica.
2) Os reatores de fusão nuclear experimentais utilizam câmaras magnéticas para conter o plasma superaquecido e para essas câmaras funcionar o campo magnético em seu interior deve ser uniforme (ou seja, com módulo constante), por esse motivo esses reatores NÃO DEVEM ser construídos de forma esférica. É por isso que eles são construídos em forma de rosquinha. (Acabamos de ver que em uma rosquinha isso é possível).
Observação do leitor Marlon sobre a consequência 2 (Adaptação):
Pelo Teorema sabemos que todo campo vetorial contínuo sobre a esfera possui um ponto onde o mesmo é nulo, por outro lado, um reator de fusão nuclear necessita de um CAMPO UNIFORME para funcionar, ou seja, o módulo do campo vetorial deve ser constante, como existe um ponto sobre a esfera onde o campo é nulo teremos que o campo é nulo em toda a esfera (se existisse um ponto não nulo então o campo não seria uniforme), assim o único campo tangente, contínuo e uniforme sobre a esfera é o campo nulo. Ora, campos magnéticos nulos não possuem aplicações práticas.
Observação do leitor Marlon sobre a consequência 2 (Adaptação):
Pelo Teorema sabemos que todo campo vetorial contínuo sobre a esfera possui um ponto onde o mesmo é nulo, por outro lado, um reator de fusão nuclear necessita de um CAMPO UNIFORME para funcionar, ou seja, o módulo do campo vetorial deve ser constante, como existe um ponto sobre a esfera onde o campo é nulo teremos que o campo é nulo em toda a esfera (se existisse um ponto não nulo então o campo não seria uniforme), assim o único campo tangente, contínuo e uniforme sobre a esfera é o campo nulo. Ora, campos magnéticos nulos não possuem aplicações práticas.
Por fim, o autor deste blog está convicto que sua batalha diária com seu "redemoinho" no alto da cabeça pode ser considerada vencida (pelo cabelo) graças à topologia!!!
Até mais pessoal!


Diego! Que maravilha este este post! É algo totalemtne novo para mim. As consequências do Teorema são bem interessantes mesmo e esclarecem muitas coisas. Você deixou um canal aberto para novas investigações. Vou procurar entender um pouco mais sobre isso.
ResponderExcluirUm forte abraço!
Realmente a matemática nunca deixa de nos surpreender com seus fatos e aplicações. Obrigado pela visita e volte sempre!!!
ResponderExcluirTinha muito tempo que não estudava matemática, como estou enferrujado, resolvi pesquisar no google, foi um grande prazer encontrar este post, parabéns leitura fácil e muito instrutiva!
ResponderExcluirWelton Vaz
ghandybh.blogspot.com
Obrigado pela visita Welton, visitei seu blog sobre Xadrez, eu gosto bastante de xadrez e seu blog é um prato cheio!!!
ResponderExcluirAté mais !
Ótima matéria!!
ResponderExcluirAliás, o conteúdo de todo o blog!
ResponderExcluirSobre o comentário em construção de reatores.
ResponderExcluirUniforme não significa contínuo, e sim com módulo constante.
Já que dado um campo tangente contínuo na esfera, deve haver um ponto onde o campo é nulo, a exigência (física) do campo ter módulo constante implica que o campo é nulo em todo ponto ( já que é nulo em 1 ponto). O único campo tangente, contínuo e uniforme sobre a esfera é o campo nulo.
Obviamente campos magnéticos nulos não têm aplicações práticas.
No mais, bom texto.
Deixo três questões como sugestões de futuros posts relacionados.
Você consegue construir um campo contínuo, tangente, e nunca nulo em S¹$? E em S³?
Como a construção de um campo tangente, contínuo e sem singularidades depende da dimensão da esfera?
Abraço,
Marlon.
Agradeço grandemente sua contribuição, já corrigi o erro presente na postagem, e gostei bastante das sugestões.
ExcluirAté mais !
Que bom ler sobre isso, Diego! Meu professor de mecânica disse que existia um teorema batizado bola cabeluda e eu não acreditei... Muito interessante.
ResponderExcluir