1) Estava estudando Análise Funcional para realizar a prova de Seleção do Programa de Doutorado em Matemática da UFC, o tempo passa muito rápido, um dia desses estava aqui no blog divulgando minha aprovação para ingressar no Mestrado, e agora não é diferente, tanto esforço valeu a pena, passei na seleção e iniciarei o Doutorado em Matemática no segundo semestre desse ano, para a minha surpresa passei em primeiro lugar no meu semestre!
2) Estou na reta final para concluir minha dissertação, última etapa para obter o grau de Mestre em Matemática, talvez eu fale um pouco do que eu abordei na minha dissertação em outra postagem.
Agora retomando as atividades, essa será a primeira de três postagens no Teoremas de Ponto Fixo.
Existem vários teoremas sobre ponto fixo, tentarei apresentar aos leitores alguns desses teoremas, alguns desses teoremas possuem uma prova um pouco mais avançada, mas tentarei ser bastante objetivo em relação à isso, a nossa motivação será encontrar aplicações desses teoremas em problemas matemáticos e no cotidiano.
Mas o que é um ponto fixo? Um ponto fixo é um ponto que não é alterado por uma aplicação, assim, o ponto fixo depende da aplicação escolhida. Por exemplo, a aplicação $f:\mathbb{R}\to\mathbb{R}$ dada por $f(x)=x^2$ possui dois pontos fixos, nesse caso $x=0$ e $x=1$. De fato,
$$f(x)=x\Leftrightarrow x^2=x\Leftrightarrow x(x-1)=0\Leftrightarrow x=0\ \mbox{ou}\ x=1 $$
É fácil ver que na aplicação identidade $Id(x)=x$ todos os pontos do domínio são pontos fixos.
O primeiro teorema sobre ponto fixo será o caso real, ou seja, nosso espaço será $\mathbb{R}$. Antes de enunciarmos o teorema, vejamos o significado geométrico do ponto fixo.
Como observamos antes, a aplicação identidade possui pontos fixos em toda reta, se considerarmos no mesmo gráfico a aplicação identidade e uma outra aplicação de $\mathbb{R}$ em $\mathbb{R}$, obtemos a seguinte figura:
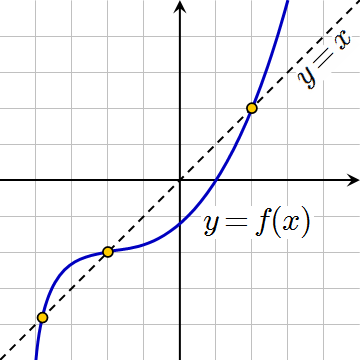 |
| Fonte: Wikipédia |
Assim, os pontos fixos são os pontos do gráfico que pertencem à imagem da aplicação identidade.
