1) Estava estudando Análise Funcional para realizar a prova de Seleção do Programa de Doutorado em Matemática da UFC, o tempo passa muito rápido, um dia desses estava aqui no blog divulgando minha aprovação para ingressar no Mestrado, e agora não é diferente, tanto esforço valeu a pena, passei na seleção e iniciarei o Doutorado em Matemática no segundo semestre desse ano, para a minha surpresa passei em primeiro lugar no meu semestre!
2) Estou na reta final para concluir minha dissertação, última etapa para obter o grau de Mestre em Matemática, talvez eu fale um pouco do que eu abordei na minha dissertação em outra postagem.
Agora retomando as atividades, essa será a primeira de três postagens no Teoremas de Ponto Fixo.
Existem vários teoremas sobre ponto fixo, tentarei apresentar aos leitores alguns desses teoremas, alguns desses teoremas possuem uma prova um pouco mais avançada, mas tentarei ser bastante objetivo em relação à isso, a nossa motivação será encontrar aplicações desses teoremas em problemas matemáticos e no cotidiano.
Mas o que é um ponto fixo? Um ponto fixo é um ponto que não é alterado por uma aplicação, assim, o ponto fixo depende da aplicação escolhida. Por exemplo, a aplicação f:\mathbb{R}\to\mathbb{R} dada por f(x)=x^2 possui dois pontos fixos, nesse caso x=0 e x=1. De fato,
f(x)=x\Leftrightarrow x^2=x\Leftrightarrow x(x-1)=0\Leftrightarrow x=0\ \mbox{ou}\ x=1
É fácil ver que na aplicação identidade Id(x)=x todos os pontos do domínio são pontos fixos.
O primeiro teorema sobre ponto fixo será o caso real, ou seja, nosso espaço será \mathbb{R}. Antes de enunciarmos o teorema, vejamos o significado geométrico do ponto fixo.
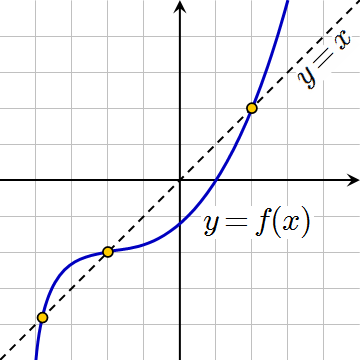
Como observamos antes, a aplicação identidade possui pontos fixos em toda reta, se considerarmos no mesmo gráfico a aplicação identidade e uma outra aplicação de \mathbb{R} em \mathbb{R}, obtemos a seguinte figura:
 |
| Fonte: Wikipédia |
Assim, os pontos fixos são os pontos do gráfico que pertencem à imagem da aplicação identidade.
Podemos pensar nos pontos fixos como um ponto de equilíbrio em uma certa situação, em Economia um Equilíbrio de Nash de um jogo é um ponto onde não há perda e nem ganhos.
Enunciamos assim o nosso primeiro teorema sobre pontos fixos.
Teorema: Seja f:[a,b]\to[a,b] uma função contínua definida em [a,b]\subset\mathbb{R}, então existe um ponto fixo em [a,b], isto é, existe x_0\in[a,b] tal que f(x_0)=x_0.
Prova: Ora, se tivermos f(a)=a ou f(b)=b não temos nada para provar. Suponha então que f(a)>a e f(b)<b.
Defina a função h:[a,b]\to[ab] por h(x)=x-f(x), note que h é contínua pois é a soma de duas funções contínuas.
Observe também que h(a)=a-f(a)<0 e h(b)=b-f(b)>0, podemos aplicar o Teorema do Valor Intermediário e concluir que existe um ponto x_0\in[a,b] tal que h(x_0)=0. Mas isso implica que x_0-f(x_0)=0, ou seja, f(x_0)=x_0.
\Box
O Blog Fatos Matemáticos tem uma postagem que aborda outras aplicações para o Teorema do ponto fixo em dimensão 1, basta clicar aqui.
Veja uma aplicação bem legal na prática do teorema ponto fixo:
Tome um elástico como o da imagem abaixo:
ax_1+b=0
ax_2+b=L
Resolvendo o sistema obtemos
a=\frac{L}{\ell}
b=-\frac{Lx_1}{\ell}
Assim, nossa função f:[0,L]\to[0,L] é definida por
f(x)=\frac{L}{\ell}(x-x_1)
E seu gráfico é
Essa função é contínua (podemos verificar isso matematicamente, mas note que seu gráfico não possui interrupções). O Teorema do ponto fixo já nos garantiu que existe pelo menos um ponto fixo e agora fica claro que tal ponto fixo é o ponto x=\frac{Lx_1}{L-\ell}.
Essa é apenas uma das aplicações em que pensei, a próxima postagem nesse assunto abordará o Teorema do Ponto Fixo em Dimensão 2! Portanto, fique atento as postagens do Giga Matemática, até mais !
Tome um elástico como o da imagem abaixo:
Agora, usando somente dois dedos segure-o dessa forma:
Estique-o o máximo que puder (cuidado para não soltar um dos lados, acredite, VAI DOER!), se considerarmos a metade superior (acima dos dedos) podemos afirmar, graças ao Teorema do Ponto Fixo, que algum ponto do elástico está na mesma posição que se encontrava antes do elástico ser esticado, incrível não é mesmo?
Mas o blog é de Matemática, nada mais justo do que uma explicação e prova matemática para essa afirmação.
Vamos lá, considere \ell o comprimento da parte superior do elástico quando este não está esticado e L o comprimento da parte superior do elástico quando este estiver totalmente esticado.
Note que "esticar o elástico" matematicamente corresponde à uma translação e uma dilatação, assim o procedimento acima corresponde à uma função da forma
f(x)=ax+b\qquad (1)
Se considerarmos o intervalo fechado [0,L] da reta, o elástico esticado corresponde ao intervalo todo, e suponha que em condição normal, a ponta esquerda está sobre o ponto x_1 e a ponta direita está sobre o ponto x_2, desse modo \ell=x_2-x_1. Veja o gráfico abaixo:
Assim, vemos que a extremidade esquerda x_1 será esticada até o ponto f(x_1)=0 e a extremidade direita x_2 será esticada até o ponto f(x_2)=L. Substituindo esse valores em (1) temos:
ax_1+b=0
ax_2+b=L
Resolvendo o sistema obtemos
a=\frac{L}{\ell}
b=-\frac{Lx_1}{\ell}
Assim, nossa função f:[0,L]\to[0,L] é definida por
f(x)=\frac{L}{\ell}(x-x_1)
E seu gráfico é
Essa função é contínua (podemos verificar isso matematicamente, mas note que seu gráfico não possui interrupções). O Teorema do ponto fixo já nos garantiu que existe pelo menos um ponto fixo e agora fica claro que tal ponto fixo é o ponto x=\frac{Lx_1}{L-\ell}.
Essa é apenas uma das aplicações em que pensei, a próxima postagem nesse assunto abordará o Teorema do Ponto Fixo em Dimensão 2! Portanto, fique atento as postagens do Giga Matemática, até mais !





O elástico (assim como qualquer outra coisa no universo observável)é formado por um número finito de átomos. Portanto, ela não é contínuo como um intervalo de reta. Isto significa que ele tem “buracos” por toda a parte. Certamente pode ocorrer do ponto $ x=\frac{Lx_1}{L-l} $ cair justamente num destes “buracos”. Isto não invalida sua aplicação?
ResponderExcluirMuito boa a sua observação Anônimo, realmente se pensarmos pelo lado físico, veremos que existem espaços vazios entre os átomos, mas isso não invalida a minha aplicação pela seguinte razão:
ResponderExcluirEu falei que um PONTO do elástico permanecerá na mesma posição, assim o elástico atua como um espaço UNIDIMENSIONAL, assim o elástico será o conjunto dos átomos e dos espaços vazios, assim como nosso universo o é, eu realmente não especifiquei se esse ponto era um átomo ou um espaço vazio.
Bem observado, então para efeitos didáticos considere o elástico como um espaço unidimensional (seus pontos são átomos e espaços vazios), levando em conta que um PONTO é uma posição no espaço, assim não importa se este é um átomo ou um espaço vazio.
Obrigado pelo comentário e volte sempre!
Caro Diego,
ResponderExcluirTenho algo interessante sobre o Teorema do ponto fixo de Bannach que requer conhecimentos de Topologia. Estava a pensar enviar para si. Que diz?
João
excelente post !!
ResponderExcluirDesde já agradeço o comentário e volte sempre!
ExcluirOlá conheci seu blog através do Educadores e Multiplicadores
ResponderExcluirSuas postagens são interessantes e esclarecedoras, e de um modo geral irá produzir frutos.
Continue nesta missão, de espalhar o conhecimento e o amor.
Deixo um mimo para você.
Uma chuva de bençãos desça sobre sua casa!
_..._ ..._(... ( ...).._
(_....__..._) _(.. ( ...)
/ (_...._) (_...._..._)\
// / / / / | \ \ \ \
/ / / / | \ \ \
/ / / / | \ \ \
♥ ♥ ♥ ♥ ♥ ♥ ♥
♥ ♥ ♥ ♥ ♥ ♥ ♥ ♥
♥ ♥ ♥ ♥ ♥ ♥
´´´, •♥♪♥♪♥♪♥♪♥♥♪♥♪♥♪♥♪♥♪♥•
´´´¢/Λ\♥♪♥♥♪♥♥♪♥♪♥♥♪♥♪♥•♥♪♥•
´´¢/.... \♥♪♥♪♥♥♪♥♪♥♥♪♥♪♥♪♥•♥*
´¢/๑۩ ๑.\♥♪♥♪♥♪♥♪♥♪♥♪♥♪♥♪♥•♥*
¢/๑۩۞۩.\´♪♥♪♥♪♥♥♪♥♪♥♪♥♪♥♪♥*
¨▓¨.♪♥♥♪.▓♥♪♥♪♥♪♥♪♥♪♥♪♥♪♥♪♥•|||||
¨▓¨.♪♥♥♪.▓¨★★★★★★★★★★★★|||
¨▓¨.♪♥♥♪.▓¨★★★★★★★★★★★★|||
¨▓¨.♪♥♥♪.▓ ★★★★★★★★★★★★|||
¨♥♥======♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥
¨♥♥======♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥♥
APDSJC!
***Lucy***
A propósito, caso ainda não esteja seguindo o meu blog deixo aqui o convite:
Fruto do Espírito
Minha Fan Page
─╔╗╦╔╗╔╗──╦╗╔═──╗╔╔╗╦╔╦╗╔╗─
─╚╗║║╦║║──║║╠═──║║║║║─║─╠╣─
─╚╝╩╚╝╚╝──╩╝╚═──╚╝╚╝╚═╚─╝╩─
P.S. Convido a conhecer o blog do irmão JC.
Mensagens atuais, algumas polêmicas, porém abençoadoras...
Acesse e confira:
Discípulo de Cristo